Research on Linear Simplification Technology of Nonlinear Cushion Packaging System II

2 Precision

In many cases, the linearization method described above can yield sufficiently accurate results in packaging engineering applications. The biggest disadvantage of using the equivalent linear method is that if B sets the excitation to be Gaussian, then non-Gaussian processes due to non-linearity cannot be obtained. In addition, equivalent linear systems may no longer be suitable when the system is subjected to certain incentives. As in the above example, if the system is subject to a frequency of 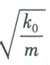For the harmonic excitation, the linearization method for the buffer package design of the tangential elastomer material described above is no longer applicable, because in this case, formula (4) will result in resonance results, which is inconsistent with the actual situation. of. One of the advantages of using a nonlinear system is that it avoids resonance. Let's analyze this issue a bit further.

Set a gentle; middle packaging system can be represented by the Duff equation of the undamped system:

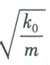
In the formula, c "1 is a small parameter; F is the amplitude of the incentive; t is the time,

The first-order approximate solution of (5) is:

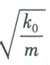
In the formula, A. For a constant, depends on the static displacement of the system at force F. Figure 1 is shown in A. : At 2cm, the system takes 0.1, 0.01, and 0.001 at e. From Fig. 1, it can be seen that when E ≥ 0.01, there is no difference in the effect of nonlinearity on the system response. However, if you do not account for the nonlinear term completely, resonance will occur in the system.

3 Conclusion

In the buffer packaging design, the linear dynamic model should be given priority, and the linear model can meet the accuracy requirements of most packaging projects. However, in the simplification of linearization, not only the size of the nonlinear term, but also the nature of the nonlinear term and the position in the mathematical model.
(Text / Zhang Minghui Sun Yong Nanchang University)

Packaging Engineering